Picture: The Development of Mathematical theory; Fundamental+New. Builds a model.
•Modern development: A lesson
learned by mathematics in the last 150 years is that it is useful to strip
the meaning away
from the mathematical assertions (axioms, postulates, propositions,
theorems) and definitions.
•One must concede the need for primitive notions, or
undefined terms or concepts, in any study. Such abstraction or formalization
makes mathematical knowledge more general, capable of multiple different
meanings, and therefore useful in multiple contexts.
•Structuralist
mathematics goes further, and develops theories and axioms (e.g. field theory, group theory, topology, vector spaces)
without any particular application in
mind.
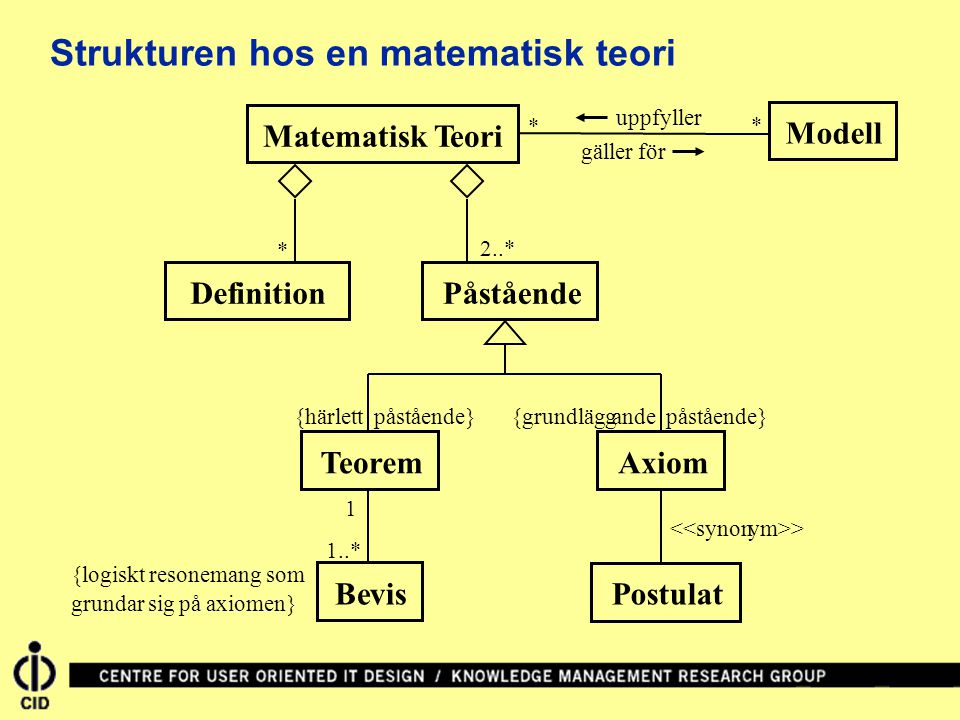
An axiom or postulate is a premise or starting point of reasoning. As classically conceived, an axiom is a premise so evident as to be accepted as true without controversy.
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems—and generally accepted statements, such as axioms.
Conclusion: A mathematical theory is a (just) building block, when we build a model of the world. The lattice for resources - a set of rules. Separate between Context (sammanhang), Content (innehåll) och
Operations can involve mathematical objects other than numbers.
* The logical values true and false can be combined using logic operations, such as and, or, and not.
* Vectors can be added and subtracted.
* Rotations can be combined using the function composition operation, performing the first rotation and then the second.
* Operations on sets include the binary operations union and intersection and the unary operation of complementation.
* Operations on functions include composition and convolution.
Quanta:
Set:
Operations on sets include the binary operations union and intersection and the unary operation of complementation.
The logical values true and false can be combined using logic operations, such as and, or, and not.
Logics: True, False. AND(A=B), OR(A+B), >,<
Group:
In mathematics, a group is an algebraic structure consisting of a set of elements together with an operation that combines any two elements to form a third element.
Arithmetic: A+B: A=Operand, +=Operation (+,-,x,/=arithmetic operators, unicode)
Unary: --1, -+1 (one operand),
Binary: 1+1 (two operands),
Ternary: If(A;True, False)
Postfix: 2!, Prefix: sin(x)
Argument:
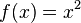, x is called an argument, and since it's one argument it's an unary function.
, is a binary function.
The number of arguments that a function takes is called the arity of the function.
Function:
Picture: f(x) is similar to f(x) = Process(Resources). Concept. Belief
Category is an algebraic structure that comprises "objects" that are linked by "arrows".
Two types of resources:
a) Type1: Is a state (finite/consumed/scarce, has potential) : Time, Money, Energy, etc
b) Type2: Is a description (meta, propagates, expressive/cognitive) : Information,
Philosophy (Information --> knowledge (epistemology) --> wisdom (fundamental insight) ---> mathematics
A codified expression is called a language (any form), which makes it cognitive - possible to become aware. Sign (can be interpreted/semiotic) or Concept (sv. begrepp/gripbar).
Research & Development precedes any robust (mathematical/fundamental) Proof of Concept.
Analyte (analytical chemistry/methods) = something you want to analyse/measure, quantitative.
Through metrology (=science of measure),
Human sensory analysis = something you can perceive/sense/feel, qualitative - good/bad for some reason.
Value lies in the ethical domain (good/bad) - as outcome - need a evaluator (stakeholder, sv. intressent).
---
The human brain has 86billion neurones and trillions of connections.
How many computers (or what software with feedback) does it takes to come up with something equivalent - with a slow moving equilibrium.
----
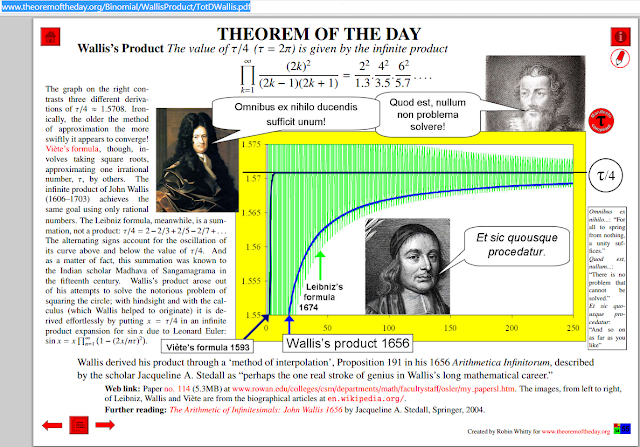
Pi found in quantum physics (Wallis product), though most efficient is Viète's formula.
---
Ethics: What you see is what you get
DNA motor: 1000x faster. Now 1/10 of what Natur can do
Expressions
Semantics is the study of meaning. Formal semantics is about attaching meaning to expressions.
Being an expression is a syntactic concept. An expression must be well-formed; 2+3 is well formed, but the expression *2+ is not.
Calculus - change, over time (requirement)
Note:
Calculus is change, and requires time.
Geometry is space, and requires time.
Algebra is
* The logical values true and false can be combined using logic operations, such as and, or, and not.
* Vectors can be added and subtracted.
* Rotations can be combined using the function composition operation, performing the first rotation and then the second.
* Operations on sets include the binary operations union and intersection and the unary operation of complementation.
* Operations on functions include composition and convolution.
Quanta:
Set:
Operations on sets include the binary operations union and intersection and the unary operation of complementation.
The logical values true and false can be combined using logic operations, such as and, or, and not.
Logics: True, False. AND(A=B), OR(A+B), >,<
Group:
In mathematics, a group is an algebraic structure consisting of a set of elements together with an operation that combines any two elements to form a third element.
Arithmetic: A+B: A=Operand, +=Operation (+,-,x,/=arithmetic operators, unicode)
Unary: --1, -+1 (one operand),
Binary: 1+1 (two operands),
Ternary: If(A;True, False)
Postfix: 2!, Prefix: sin(x)
Argument:
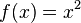, x is called an argument, and since it's one argument it's an unary function., is a binary function.The number of arguments that a function takes is called the arity of the function.
Function:
Picture: f(x) is similar to f(x) = Process(Resources). Concept. Belief
Category is an algebraic structure that comprises "objects" that are linked by "arrows".
a) Type1: Is a state (finite/consumed/scarce, has potential) : Time, Money, Energy, etc
b) Type2: Is a description (meta, propagates, expressive/cognitive) : Information,
Philosophy (Information --> knowledge (epistemology) --> wisdom (fundamental insight) ---> mathematics
A codified expression is called a language (any form), which makes it cognitive - possible to become aware. Sign (can be interpreted/semiotic) or Concept (sv. begrepp/gripbar).
Research & Development precedes any robust (mathematical/fundamental) Proof of Concept.
Analyte (analytical chemistry/methods) = something you want to analyse/measure, quantitative.
Through metrology (=science of measure),
Human sensory analysis = something you can perceive/sense/feel, qualitative - good/bad for some reason.
Value lies in the ethical domain (good/bad) - as outcome - need a evaluator (stakeholder, sv. intressent).
---
The human brain has 86billion neurones and trillions of connections.
How many computers (or what software with feedback) does it takes to come up with something equivalent - with a slow moving equilibrium.
----
Pi found in quantum physics (Wallis product), though most efficient is Viète's formula.
---
Ethics: What you see is what you get
DNA motor: 1000x faster. Now 1/10 of what Natur can do
Expressions
Semantics is the study of meaning. Formal semantics is about attaching meaning to expressions.
Being an expression is a syntactic concept. An expression must be well-formed; 2+3 is well formed, but the expression *2+ is not.
Calculus - change, over time (requirement)
Note:
Calculus is change, and requires time.
Geometry is space, and requires time.
Algebra is
Calculus is the mathematical study of change, in the same way that geometry is the study of shape and algebra is the study of operations and their application to solving equations. It has two major branches, differential calculus (concerning rates of change and slopes of curves),[1] and integral calculus (concerning accumulation of quantities and the areas under and between curves);[2] these two branches are related to each other by the fundamental theorem of calculus. Both branches make use of the fundamental notions of convergence of infinite sequences and infinite series to a well-defined limit. Generally, modern calculus is considered to have been developed in the 17th century by Isaac Newton and Gottfried Leibniz. Today, calculus has widespread uses in science, engineering andeconomics[3] and can solve many problems that algebra alone cannot.
Calculus is a part of modern mathematics education. A course in calculus is a gateway to other, more advanced courses in mathematics devoted to the study offunctions and limits, broadly called mathematical analysis. Calculus has historically been called "the calculus of infinitesimals", or "infinitesimal calculus". The word "calculus" comes from Latin (calculus) and refers to a small stone used for counting. More generally, calculus (plural calculi) refers to any method or system of calculation guided by the symbolic manipulation of expressions. Some examples of other well-known calculi are propositional calculus, calculus of variations,lambda calculus, and process calculus.
No comments:
Post a Comment